Ottimizzazione Industriale & Logistica

Ricerca Operativa (Ingegneria) A.A. 2000/2001

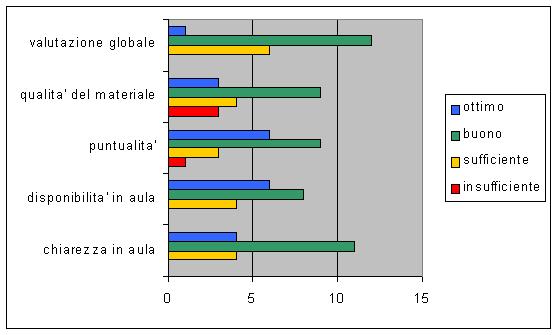
Valutazione Corso

Orario

Martedì dalle ore 10.30 alle ore 12.30 AULA B 0.12
Mercoledì dalle ore 10.30 alle ore 13.30 AULA B 0.12
Giovedì dalle ore 15.00 alle ore 18.00 AULA B 0.12

Top

Lezioni

XII settimana

martedì 15 maggio 2001
Esercitazione sull'algoritmo di Ford-Fulkerson.

mercoledì 16 maggio 2001
Gestione di un progetto tramite reti di attività. Cammino critico, attività critica. Allocazione di risorse a costo minimo (CPM): formulazione come PL.

giovedì 17 maggio 2001
Duale di CPM. Soluzione tramite simplesso su reti.

XI settimana

martedì 8 maggio 2001
Metodo Primale-Duale per il problema del cammino minimo. Esempi.

mercoledì 9 maggio 2001
Problema del massimo flusso. Formilazione come caso particolare di flusso ottimo. Duale del massimo flusso. Tagli, s-t tagli, capacità di un taglio. Duale del massimo flusso come problema di taglio minimo. Teorema max-flow min-cut.Algoritmo primale-duale (s-t cammini aumentanti, condizioni di ottimalità). Algoritmo di Ford-Fulkerson.

giovedì 10 maggio 2001
Metodo dei Piani di Taglio. Applicazione al problema dell'arborescenza ricoprente ottima e al TSP.L'algoritmo di Ford-Fulkerson come oracolo di separazione.
Metodo di Branch-and-Bound. Applicazione al Knapsack intero.

X settimana

mercoledì 2 maggio 2001
Problema del cammino minimo. Formulazione come problema di flusso e come problema combinatorico. Matrice unimodulare e totalmente unimodulare. Condizione necessaria e condizione sufficiente di totale unimodularità. Soluzione del cammino minimo con il simplesso. Cammino minimo su grafi diretti con cicli negativi.

giovedì 3 maggio 2001
1. Algoritmo label correcting (complessità e applicabilità). Algoritmo label setting (Dijkstra) come caso particolare di label correcting (applicabilità, complessità, correttezza). Estensione a funzioni peso definite come: (i) prodotto dei pesi del cammino: minimizzare la probabilità di perdita di un pacchetto in una rete TLC. (ii) peso massimo di un arco del cammino: minimizzare la pendenza massima incontrata in un tragitto da s a t.

IX settimana

giovedì 26 aprile 2001
Metodo del simplesso su reti. Aggiornamento della soluzione corrente. Determinazione di una soluzione iniziale. Basi degeneri e problemi di convergenza. Esempi.

VIII settimana

mercoledì 18 aprile 2001
Problemi multiobiettivo: soluzioni non dominate.
Esercitazione: Acquistare l'auto ideale.
Introduzione ai Problemi di Flusso: Flusso Ottimo, Problema di Trasporto, Massimo Flusso, Cammino Minimo

giovedì 19 aprile 2001
Problema dei trasporti: metodo del simplesso su reti. Basi e soluzioni di base. Costi ridotti e criterio di ottimalità. Esempi.

VII settimana

martedì 10 aprile 2001
Esercitazione: Gestione di un portafoglio di titoli. Giochi a somma zero.

mercoledì 11 aprile 2001
Il metodo Primale-Duale. Esempi.

VI settimana

martedì 3 aprile 2001
Il metodo del simplesso: criteri di ottimalità e illimitatezza. Miglioramento della base corrente. Esercizi ed esempi.

giovedì 5 aprile 2001
Calcolo di una base iniziale: il metodo delle variabili artificiali. Esercizi ed esempi.

V settimana

mercoledì 28 marzo 2001
geometria del simplesso: involucro convesso, cono di recessione, basi, vertici, punti estremi e teorema fondamentale della PL.

giovedì 29 marzo 2001
Simulazione di una negoziazione tra impianti industriali. Interpretazione economica del duale di un problema di PL.

IV settimana

martedì 20 marzo 2001
Problemi di PL in forma generale. Sistemi di disequazioni lineari. Compatibilità e incompatibilità. Diseguaglianze implicate. Come determinare se un poliedro è vuoto. Proiezione di poliedri e sistemi di diseguaglianze equivalenti. Teorema di Fourier. Metodo di Fourier-Motzkin. Esempio ed esercitazione.

mercoledì 21 marzo 2001
Elementi di teoria della complessità computazionale. Teoria della dualità. Teorema della dualità forte. Problema primale e problema duale. Dualità debole. Formulazione del problema duale di un generico problema di PL. Interpretazione economica del problema duale. Variabili duali e prezzi ombra in un sistema economico all’equilibrio.

giovedì 22 marzo 2001
Dualità debole, reciprocità, condizioni di complementarità. Soluzione di un problema di PL tramite Fourier-Motzkin. Esercitazione: simulazione di una competizione commerciale tra sistemi di produzione.

III settimana

martedì 13 marzo 2001
Matrode grafico. Proprietà delle matrici di incidenza di grafi orientati: rango, caratterizzazione delle matrici di base. Relazione tra matroide grafico e matroide lineare. Esempi.
mercoledì 14 marzo 2001
Algoritmo greedy e Teorema di Rado. Applicazioni ed esempi. Intersezione di due e di tre matroidi. Problema del matching bipartito.

giovedì 15 marzo 2001
Complessità di un algoritmo, complessità di un problema. Le classi P e NP. Esempi. Riduzioni polinomiali: problemi NP-completi. Esempio di riduzione: clique.

II settimana

martedì 6 marzo 2001
Grafi planari, intervallo, bipartiti. Colorazione di un grafo, clique e insieme stabile. Percorsi e cammini: connessione. Grafi regolari. Cicli e circuiti: caratterizzazione dei grafi bipartiti.
mercoledì 7 marzo 2001
Grafi privi di cicli: alberi e foreste. Rappresentazione matriciale di grafi: matrici di adiacenza e di incidenza. Esempi. Ipergrafi. Definizione formale di problema di certificazione, combinatorico, di ottimizzazione combinatoria. Sistemi di indipendenza. Matroidi. Esempi: matroide uniforme, knapsack.
giovedì 8 marzo 2001
Elementi di geometria di Rn. Combinazione lineare, affine, conica, convessa. Dipendenza e indipendenza lineare (affine). Involucri. Esempi. Basi e Teorema di Steinitz. Matroide lineare.

I settimana

martedì 27 febbraio 2001
Introduzione al corso. Origine della Ricerca Operativa. Modelli e problemi di ottimizzazione. Esempi: il problema della dieta.
mercoledì 28 febbraio 2001
Riferimenti bibliografici. Ottimizzazione lineare, non lineare, combinatoria. Esempi: gestione di turni, traiettoria ottimale.
giovedì 1° marzo 2001
Esempi di problemi di ottimizzazione combinatoria: assegnazione di aule e colorazione di una carta geografica come colorazione di un grafo. Elementi di teoria dei grafi: definizioni fondamentali. Grado di un vertice e teorema di Eulero (enunciato).
Martedì dalle ore 10.30 alle ore 12.30 AULA B 0.12
Mercoledì dalle ore 10.30 alle ore 13.30 AULA B 0.12
Giovedì dalle ore 15.00 alle ore 18.00 AULA B 0.12

Top

Orario di Ricevimento

Mercoledì dalle ore 12.00 alle ore 13.00
Giovedì dalle ore 15.00 alle ore 16.30

Top

Appelli

I° Appello
Martedì 5 Giugno 2001 ore 10.30 Aula 1.6 Coppito 1
II° Appello
Martedì 26 Giugno 2001 ore 10.30 Coppito 1
Venerdì 20 Luglio 2001 ore 10.30 Coppito 1

III° Appello
18 settembre 2001 ore 10.30 Prova scritta. Orale a seguire

IV° Appello
23 ottobre 2001 ore 10.00 Prova scritta Aula A-1.7. Orale da definire
18 dicembre 2001 ore 10.30 Prova scritta. Orale ore 15.30

V° Appello
Lunedì 25 febbraio ore 17.00 aula B014

Top

Programma

Modelli di ottimizzazione
Problemi lineari e non lineari, problemi in spazi infinito dimensionali. Esempi: progettazione di un amplificatore a retroazione, ottimizzazione dei livelli produttivi in un'industria, problema della dieta, problemi di trasporto [3].

Problemi combinatorici
Cammino minimo, minimo albero ricoprente [2]. Elementi di algebra lineare: dipendenza e indipendenza lineare, insiemi massimali, basi; unicità della rappresentazione in una data base, lemma di Steinitz [1].

Sistemi di indipendenza
Assiomi per sistemi di indipendenza. Assioma di scambio, matroidi. Esempi. Caratterizzazione algoritmica dei problemi di ottimizzazione combinatoria con struttura matroidale [2,4].
Matroide lineare, grafico, partizione. Esempi [2,4].

Programmazione lineare
Relazioni tra problemi di ottimizzazione in Rn, di ottimizzazione combinatorica e di programmazione lineare (PL). Combinazione conica, affine, convessa. Esempi. Problemi di PL in forma generale. Sistemi di disequazioni lineari. Compatibilità e incompatibilità. Diseguaglianze implicate [1,2].
Come determinare se un poliedro è vuoto. Proiezione di poliedri e sistemi di diseguaglianze equivalenti. Teorema di Fourier. Metodo di Fourier-Motzkin. Esempi [1].

Teoria della dualità
Teorema della dualità forte. Problema primale e problema duale. Dualità debole [1,2].
Teoria della dualità [1]. Cenni alle estensioni e alle applicazioni in matematica combinatoria e teoria degli algoritmi. Formulazione del problema duale di un generico problema di PL.

Applicazioni
Interpretazione economica del problema duale. Variabili duali e prezzi ombra in un sistema economico all'equilibrio [3].
Un modello lineare di teoria dei giochi: giochi a somma zero. Problemi min-max e max-min. Formulazione come coppia primale-duale [3]. Un metodo di soluzione generale per problemi di PL basato sulla dualità forte e sul Teorema di Fourier-Motzkin [1,2].
Curve di regressione; determinazione della retta di regressione associata a una nuvola di punti nel piano; linearizzazione del modulo e formulazione come problema di PL [3].

Metodo del simplesso
Definizione di base di un problema di PL. Soluzioni di base ammissibili. Supporto di una soluzione (di base). Soluzioni di base degeneri. Equivalenza tra soluzioni di base ammissibili e vertici di un poliedro. Esempi. Forma canonica di un problema di PL. Esempi. Costi ridotti. Criteri di illimitatezza e ottimalità [1].
Il simplesso: dimostrazione del teorema di correttezza; determinazione di una base iniziale; soluzioni degeneri. Il problema della convergenza del metodo del simplesso. Problema perturbato e teoremi di convergenza [1].
Il metodo primale-duale per la programmazione lineare. Esempi [2].

Programmazione lineare intera
Esempi: formulazione di knapsack intero e del problema del commesso viaggiatore. Matrici unimodulari e totalmente unimodulari. Una condizione per l'interezza delle soluzioni di base in un problema in forma standard [2].
Condizioni di interezza per problemi in forma generale. Un criterio di unimodularità totale. Esempi: il problema del cammino minimo [3].

Casi reali
Il problema della gestione di un magazzino industriale. Costi di riordine, movimentazione e trasporto, costi di handling e stoccaggio. Frequenza singola, multifrequenza, consolidamento. Formulazione come problema di programmazione lineare intera. Problemi time-indexed: formulazione come cammino ottimo [2].

Ottimo su reti
Flusso e divergenza di un campo conservativo. Campi discreti e reti. Distribuzione di flusso e potenziale. Problemi di flusso ottimo. Problemi separabili. Esempi: problema del trasporto, problema del cammino minimo, problema del flusso massimo [4].
Il metodo del simplesso per problemi di trasporto. Determinazione di una base iniziale. Soluzioni di base ammissibili. Calcolo dei potenziali e dei costi ridotti. Pivoting e ammissibilità primale. Soluzioni degeneri. Considerazioni sul'efficienza del metodo [5].
Il problema dell'(s,t)-cammino di peso minimo. Confronto tra simplesso e metodo di Dijkstra. Il metodo di Dijkstra come caso particolare del metodo primale-duale. Formulazioni alternative con separazione di (s,t)-tagli [2,4].
Esempi: sintesi ottima di reti di telecomunicazione. Allocazione delle capacita' a fronte di domanda deterministica. Modelli di costo (discreto, convesso, lineare con costi di attivazione, lineare) [2].
Il problema del flusso massimo. Formulazione primale come flusso a minimo costo. Formulazione duale. Interpretazione delle soluzioni duali: taglio di capacità minima e teorema di Ford-Fulkerson [4].
Problemi di abbinamento. Il caso bipartito. Confronto tra i problemi di cammino minimo, taglio minimo e matching bipartito [3]. Gerarchia di problemi di flusso e approccio continuo a problemi di ottimizzazione combinatoria [4].
Abbinamento perfetto: il caso non pesato. Cammini alternanti e aumentanti. Teorema e algoritmo di Edmonds [2,4]. § Problemi pesati. Diseguaglianze valide. Teorema di Edmonds sul poliedro del matching non bipartito (enunciato) [4]. Individuazione di cicli dispari e diseguaglianze violate [2].
Formulazione di cammino minimo come matching bipartito perfetto [2].
Tecniche di programmazione reticolare e Project Management. PERT e metodo del cammino critico. Pareto-ottimalità e analisi delle soluzioni non-dominate [7].

Elementi di teoria delle code
Relazioni fondamentali. Sistemi M/M/1. Paradosso del tempo di attesa. Sistemi M/G/1 [7].

Metodi di generazione di colonne
Problemi di cutting stock. Modelli fondamentali. Obiettivi e vincoli. Complessità. Formulazioni in termini di programmazione lineare intera. Esempi [2,3].
Metodi di generazione di colonne per la soluzione di problemi di cutting stock [2].

Top

Testi di Riferimento

A. Sassano, Modelli e Algoritmi della Ricerca Operativa, Franco Angeli Ed. (1999)

A. Agnetis, C. Arbib, M. Lucertini, S. Nicoloso, Il Processo Decisionale, Nuova Italia Scientifica (1992)

C.H. Papadimitriou, K.E. Steiglitz, Combinatorial Optimization, Algorithms and Complexity, Prentice Hall (1982)

Ahuja, Magnanti, Orlin, Network Flows

E. Lawler, Combinatorial Optimization: Networks and Matroids

Top

Materiale Didattico Integrativo

C. Arbib, Appunti delle lezioni, dispense in distribuzione

S. De Julio, A. La Bella, Elementi di Teoria delle File d'Attesa, dispense in distribuzione

C. Arbib, F. Marinelli, Sistemi di Disequazioni Lineari (il Metodo di Fourier-Motzkin), (in formato presentazione PowerPoint oppure come file PostScript)

C. Arbib, Teoria della Dualità (in formato presentazione PowerPoint oppure come file PostScript)

C. Arbib, Simulazione di una Negoziazione tra Sistemi di Produzione (Esercitazione) (in formato presentazione PowerPoint oppure come file PostScript)

C. Arbib, F. Marinelli, il Metodo del Simplesso, (in formato presentazione PowerPoint oppure come file PostScript)

C. Arbib, Gestione di un portafoglio di titoli (Esercitazione) , (in formato presentazione PowerPoint oppure come file PostScript)

C. Arbib, S. Smriglio, il Metodo Primale-Duale, (in formato presentazione PowerPoint oppure come file PostScript)

C. Arbib, Acquistare l'auto ideale (Esercitazione), (in formato presentazione PowerPoint oppure come file PostScript)

F. Marinelli, L'algoritmo di Ford-Fulkerson (Esercitazione), (in formato presentazione PowerPoint oppure come file PostScript)

Top

Temi di Esame

I temi di esame sono gli stessi dei corsi Ricerca Operativa (Inf.- Mat.) e Ricerca Operativa II

Top

Bacheca

non ci sono avvisi particolari

Top