Ricerca Operativa

Esercitazione per la prova parziale del 12.02.2002

Quesiti 1-6 a risposta multipla: selezionare, per ogni quesito, tutte le risposte corrette.

1. Una coppia (U, Á) con U insieme finito e Á Í 2^U si dice matroide se

A) Á gode della proprietà di scambio

B) Á è subclusiva e gode della proprietà di scambio

C) Á è subclusiva e i suoi massimali hanno tutti lo stesso numero di elementi

2. Un matching in un grafo simmetrico è

A) un insieme di nodi a due a due non adiacenti

B) un insieme di archi a due a due non adiacenti

C) un insieme massimale di archi a due a due non adiacenti

3. In un grafo simmetrico un insieme stabile massimale

A) è sempre massimo

B) è sempre dominante

C) è sempre ricoprente

4. I matching di un grafo bipartito

A) godono in generale della proprietà di scambio

B) sono sempre perfetti

C) non godono in generale della proprietà di scambio

5. La proiezione in IR^(n–1) di un poliedro di IRⁿ è sempre

A) un insieme convesso

B) un poliedro limitato

C) l’insieme vuoto

6. Un grafo è bipartito se

A) l’insieme dei suoi vertici si può partizionare in due clique

B) non contiene cicli dispari

C) ammette un matching perfetto

Quesiti 7-9 a risposta aperta

7. Il seguente algoritmo ha come scopo il calcolo della massima clique Q di un grafo simmetrico

G = (V, E):

0) Q := Æ; U := V;

1) se U = Æ, stop;

2) tra i vertici di U che sono adiacenti a tutti i vertici di Q, scegline uno di grado massimo e aggiungilo a Q;

3) togli il vertice scelto da U e torna al passo 1.

Costruire un grafo in corrispondenza al quale l’algoritmo fornisce una clique di dimensioni inferiori al massimo.

8. Due giocatori di scacchi vogliono disporre su una scacchiera un ugual numero di torri bianche e nere in modo 1) ogni torre occupi una casa del proprio colore 2) nessuna torre si trovi sotto scacco di una torre di diverso colore. Qual è il massimo numero di torri che possono collocare? Formulare la questione come problema di ottimizzazione combinatoria, specificando l’insieme universale, la proprietà caratteristica degli insiemi ammissibili e la funzione peso.

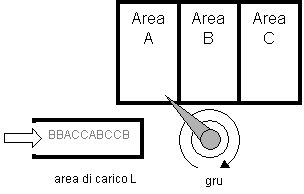
9. Un impianto industriale utilizza una gru per spostare dei pezzi da una zona all’altra dell’officina. I pezzi pervengono alla gru in un medesimo punto L dell’impianto dove si accumulano in un ordine stabilito (non modificabile), e hanno diverse destinazioni a seconda della loro tipologia: i pezzi di tipo A devono raggiungere la zona A, quelli di tipo B la zona B e così via. La gru può prelevare fino a 3 pezzi contemporaneamente. Se ad esempio l’ordine di arrivo dei pezzi è BCCBACCABB, la gru potrà eseguire una prima missione portando i pezzi BCC, poi una seconda portando BA, una terza portando CC e una quarta portando ABB. La durata di una missione dipende dal tempo necessario a raggiungere l’area più lontana. Se l’area A dista 1, l’area B dista 2 e l’area C dista 3 dall’area di carico L, la missione BCC durerà 3, la missione BA 2, la missione CC ancora 3 e la missione ABB ancora 2. La durata totale si ottiene sommando le varie durate, e dunque se si decide di smistare il carico attraverso le 4 missioni ipotizzate occorrerà un tempo pari a 10. Si formuli il problema di ottimizzazione combinatoria consistente nell’individuare un insieme ammissibile di missioni che abbia durata complessiva minima.