RICERCA OPERATIVA GRUPPO D

prova scritta intermedia del 12 febbraio 2002

Rispondere alle seguenti domande. Nelle domande a risposta multipla marcare a penna la lettera corrispondente alla risposta ritenuta corretta (una sola tra quelle riportate). Ogni risposta esatta vale 2 punti.

1. Se un insieme S è massimale rispetto a una proprietà Ã

A) S è il più grande insieme che verifica la proprietà Ã

B) esiste un x Ï S tale che S È {x} non verifica la proprietà Ã

C) S È {x} non verifica la proprietà Ã per ogni x Ï S

2. Applicato a un albero, l’algoritmo greedy per la massima clique

A) trova una soluzione ottima

B) non trova in generale una soluzione ottima

C) non può essere applicato

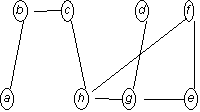
3. Indicare un edge-cover minimo e un edge-

cover minimale che non è minimo nel grafo di figura.

Minimo: {ef, gd, ch, ab}

Minimale non minimo: {bc, hg, ef, gd, ab}

4. Le colonne linearmente indipendenti della matrice di incidenza nodi-archi di un grafo orientato

A) corrispondono ad alberi ricoprenti

B) corrispondono ad archi che formano cicli

C) corrispondono ad archi che non formano cicli

5. Una combinazione lineare l₁a₁ + l₂a₂ + … + l_ka_k si dice affine se

A) la somma dei coefficienti l_i è pari a 1

B) i coefficienti l_i sono non tutti nulli

C) i coefficienti l_i sono tutti non negativi

6. Quale dei seguenti insiemi di nodi può sempre essere calcolato con l’algoritmo greedy in un grafo bipartito connesso?

A) il massimo insieme stabile

B) il massimo matching

C) la massima clique

RICERCA OPERATIVA GRUPPO D

Risolvere i seguenti problemi. Ogni problema viene valutato da 0 a 6 punti.

7. Siano a e b due numeri interi positivi, e sia U = {u₁, …, u_n} un insieme finito. Dati A, B Í U, si consideri la famiglia Á di tutti i sottoinsiemi X di U tali che |X – A| < a e |X – B| < b. Dire se tale famiglia

• è subclusiva
• gode della proprietà di scambio

e spiegare il perché:

è/non è subclusiva perché: se Y Í X e |X – A| < a, |X – B| < b, allora anche |Y – A| < a e |Y – B| < b

gode/non gode della proprietà di scambio perché: Siano X = {x}, Y = {y, z}, A = {y}, B = {z},

a = b = 2. X e Y appartengono banalmente a Á. Ma per X’ = X È {y} = {x, y} si ha |Y’ – B| = |Y’| = 2; per X” = X È {z} = {x, z} si ha |X” – A| = |Y”| = 2. Quindi non vale la proprietà di scambio.

8. In un circuito elettronico integrato, i componenti hanno forma rettangolare e sono disposti con i lati a un sistema di assi cartesiani ortogonali. Dati due componenti qualsiasi A e B, è possibile collegarli soltanto tramite un segmento di linea retta parallelo agli assi con un estremo su A e l’altro su B. Ci si chiede quale sia il più grande insieme di componenti che non è possibile collegare tra di loro in alcun modo. Formulare il problema in termini di ottimizzazione combinatoria su un opportuno grafo G. Specificare: l’insieme V dei vertici del grafo, l’insieme E dei suoi archi, l’insieme universo U, la famiglia Á delle soluzioni ammissibili e la funzione peso c.

ogni vÎV corrisponde a	un componente del circuito
uvÎE se e solo se	il componente u e il componente v sono visibili l’uno dall’altro
l’insieme U è formato da	i vertici di G
XÎÁ se e solo se	X è un insieme stabile
"xÎU, c(x) vale	1 (max)

9. Descrivere il poliedro di IR² che si ottiene proiettando il seguente poliedro P nello spazio delle variabili x₁, x₂:

3x₁ – 2x₂ + x₄ < 6

2x₁ + x₂ + x₃ < 2

2x₁ + 3x₃ > 6

x₁ + x₂ + x₄ < 3

Calcolare inoltre le coordinate di un punto di P (se esiste).

Poliedro: 4x1 + 3x2 < 0

Eventuale soluzione: x1 = x2 = 0 x3 = 2 x4 = 3