RICERCA
OPERATIVA GRUPPO B
prova
scritta intermedia del 12 febbraio 2002
Rispondere alle seguenti
domande. Nelle domande a risposta multipla marcare a penna la lettera
corrispondente alla risposta ritenuta corretta (una sola tra quelle riportate).
Ogni risposta esatta vale 2 punti.
1. Se Y Î Á e vale la proprietà di subclusione
A) X Î Á
B) X e Y godono
della proprietà di scambio per ogni X Ì Y
C) i massimali sono tutti non vuoti
2. Applicato a un grafo bipartito connesso, l’algoritmo greedy per la massima clique
A) trova una soluzione ottima
B) non trova in generale una soluzione ottima
C) non può essere applicato
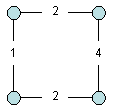
3. Mostrare le fasi di esecuzione di un algoritmo greedy
applicato alla ricerca di un albero ricoprente di peso
minimo nel grafo di figura.
Nell’ordine
l’algoritmo seleziona gli archi:
de, gf, cd,
dg, ab, gh, bc
La soluzione trovata è ottima?
Se sì, perché? È
un matroide grafico
Se no, perché?
4. Le colonne linearmente dipendenti della matrice di incidenza nodi-archi di un grafo orientato
A) corrispondono ad alberi ricoprenti
B)
corrispondono ad archi che
formano cicli
C) corrispondono ad archi che non formano cicli
5. Un insieme di vettori è linearmente dipendente se
A) contiene l’insieme vuoto
B) non è massimale
C)
contiene il vettore nullo
6. Quale dei seguenti insiemi di archi di un grafo non costituisce una famiglia subclusiva?
A) archi che formano sottografi bipartiti
B)
archi che formano circuiti
hamiltoniani
C) archi che formano matching
RICERCA
OPERATIVA GRUPPO
B
Risolvere i seguenti problemi.
Ogni problema viene valutato da 0 a 6 punti.
7. Sia G = (V, E) un grafo
simmetrico e c: E à IR+. Quale
problema risolve il seguente algoritmo?
0)
Q
:= E; U := E;
1) se U = Æ, stop;
2)
scegli
x Î U con c(x)
< c(u) "uÎU;
3) se "vÎV $y Î Q – {x}tale che vÎy, poni Q := Q – {x};
4)
poni
U := U – {x} e torna al passo 1.
Disegnare un grafo in
corrispondenza al quale l’algoritmo non trova una soluzione ottima.
|
Problema risolto |
edge-cover |
|
Grafo |
|
8. I sette nani combinatorici
(Angolo, Broccolo, Circolo, Dondolo, Eccolo, Finferlo, Giotto) hanno deciso che
per la festa di Biancaneve vestiranno in modo particolare: ogni nano dovrà
avere il cappello di colore diverso dai calzoni, e non vi dovranno essere due
nani con calzoni del medesimo colore, né due nani con cappello del medesimo
colore. Poiché non è detto che vi siano calzoni e cappelli di colori
sufficienti, forse non tutti i nani potranno partecipare alla festa. Formulare
il problema di massimizzare il numero di nani in grado di rispettare la
condizione voluta, indicando nella seguente tabella insieme universale U,
proprietà Ã delle soluzioni ammissibili
e funzione peso c.
|
l’insieme U è
formato da |
coppie (colore
calzoni, colore cappello) con il colore dei calzoni
diverso da quello del cappello |
|
XÎÁ
se e solo se |
X è un insieme
di coppie che non hanno oggetti comuni |
|
"xÎU, c(x) vale |
1 (max) |
9. Dire se il seguente
sistema di disequazioni lineari
3x1
+ x2 – 2x4
< 4
x1 – 2x2 + x3 <
2
x2 – 4x3 > 6
x1 + x2
+ x3 = 3
ammette
o no soluzioni in IR4, e in caso affermativo esibire una soluzione.
|
il sistema |
non ammette soluzione | | |
|
ammette la seguente soluzione: x1 = 49/12, x2 = 1/3 , x3 = –17/12, x4
= 103/24 |